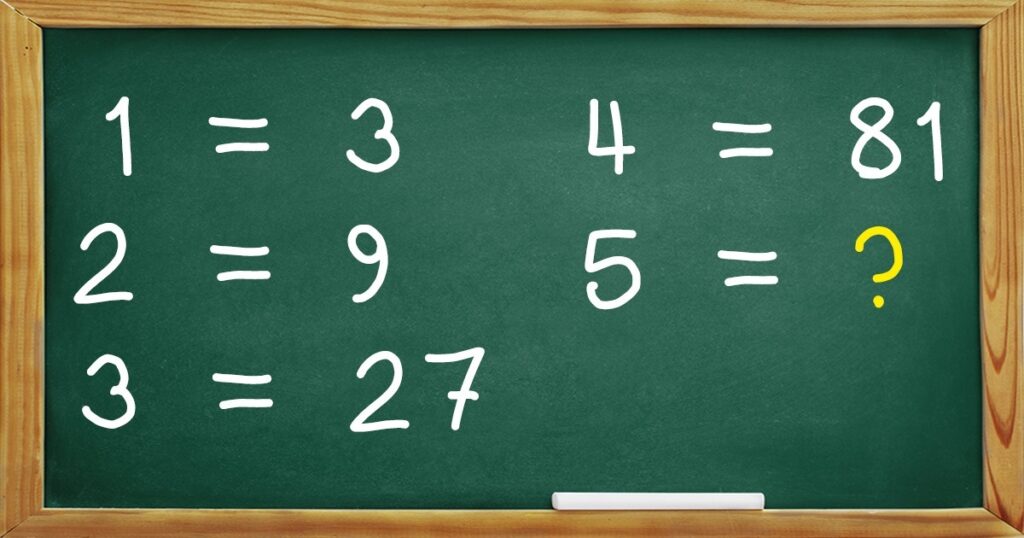Demonstrează-ți talentul la matematică, pe care probabil l-ai ascuns tot timpul. La urma urmei, anii de școală rămân în urmă, iar teoremele lui Pitagora rămân în capul tău. Și dacă te întrebai cum se pot folosi aceste teoreme în viața de zi cu zi, găsește mai jos exemplul.
Exercițiile sunt pe niveluri – de la cel mai ușor la cel mai complex.
Nivelul 1
Să începem cu cele mai simple.Fără a utiliza un calculator, rezolvă exemplul următor.
Te-ai descurcat? La nivelul următor, aplică, pe lângă abilitățile matematice, și ingeniozitatea.
Nivelul 2
FOLLOW ME
Odată, un indian numit Pero Altruist a servit poporului său. El a exterminat infractorii și i-a ajutat pe cei săraci. Avea un revolver cu 6 gloanțe. Intervalul dintre prima și a șasea lovitură era de 5 secunde. Când se plimba prin sat, a văzut un băiat tânăr, desculț urmărit de trei bandiți. Singura modalitate de a salva copilul este de a împușca bandiții. Altruist a calculat că are doar 2 secunde să o facă.
Î: Este suficient timp ca el să tragă de 3 ori?
Nivelul 3
Două trenuri se mișcă în direcții opuse. Unul dintre ele de la Praga la Moscova, al doilea – de la Moscova la Praga. Ele vor ajunge la destinație într-o oră și respectiv 4 ore, după ce se vor întâlni.
Întrebare: Cât de repede va ajunge unul dintre trenuri? De ce?
Nivelul 4
Un angajat responsabil cu spălatul ferestrelor a venit la o corporație mare pentru a-și face treaba. Avea o scară lungă de 25 m care se afla la 7 m de la baza clădirii. Dar partea superioară a scării a coborât până la 4 m. Pentru a o menține stabilă pe podea, este necesar să o fixeze la o anumită distanță de perete.
Întrebare: La ce distanță de perete se află scările după alunecare ?
Nivelul 5
Nivelul 1
Rezultatul tău a fost 12? Sau poate 1? Din păcate, ambele răspunsuri sunt greșite.
Răspuns corect: 30. Fii atent la felul în care sunt așezate numerele în imagine, între ultimul 1 de pe rând și primul de pe rândul următor nu există niciun semn. Deci, aceste cifre sunt de fapt 11, care pur și simplu nu a încăput pe un singur rând.
Nivelul 2
Da, de data asta va fi suficient timp pentru a-l salva pe copil. Iată soluția:
5 secunde / 6 = 0,833 sec.
0,833 sec. * 3 = 2,5 secunde.
Nivelul 3
Se presupune că ambele trenuri se mișcă cu o viteză constantă, iar șinele sunt paralele și au aceeași lungime. Este, de asemenea, cunoscut faptul că încep să se miște în același timp. Cursul soluției este după cum urmează:
Avem 2 distanțe X și Y de la „punctul de întâlnire” la cele două puncte finale. Un tren A necesită 1 oră pentru a conduce vehicul Y distanță, iar trenul B – 4 ore pentru X distanță. Astfel, viteza trenului A este egal cu (Y / 1 = Y), iar viteza trenului B este (X / 4).
Trenul A are nevoie de același timp pentru distanța X (cu viteza Y) și trenul B pentru distanța Y (cu viteza X / 4).
Timpul scurs înainte de punctul de întâlnire este aceeași pentru ambele și rezultă un raport al distanțelor X și Y: X / Y = 4Y / X ⇒ X * X / Y = 4Y ⇒ X * X = 4Y * Y ⇒ X = 2Y.
După aceasta, putem spune că, dacă viteza trenului A este Y, atunci viteza trenului B ar trebui să fie (2Y / 4) = Y / 2.
Aceasta înseamnă că trenul A este de 2 ori mai rapid decât trenul B. Și s-au întâlnit la 2 ore de la pornire, când trenul A parcursese deja 2/3 din distanță, în timp ce trenul B parcursese numai 1/3.
Nivelul 4
Răspuns: 15 m.
Zidul, podeaua și scara formează un triunghi dreptunghic. Scara este o ipotenuză, iar peretele și podeaua sunt catetelr. Pentru triunghiuri cu un unghi drept se folosește teorema lui Pitagora, care prevede că suma pătratelor lungimilor catetelor este egală cu pătratul ipotenuzei. Pentru o scară de 25 m lungime, pătratul său este de 625 de metri pătrați. Și pătratul uneia dintre catete este de 49 de metri pătrați. Aceasta înseamnă că pătratul catetei, reprezentate de zid, este de 625 – 49 = 576 mp. Prin urmare, lungimea catetei reprezentată de perete , adică înălțimea sa, este egală cu √576 = 24 m. În cazul în care scara alunecă în jos pe perete la 4 m, înălțimea va fi redusă la 20 m.
Nivelul 5
Toate numerele din rândul din dreapta sunt grade diferite ale numărului 3. 3 este 3 în primul grad, 9 în al doilea, 27 în al treilea, 81 în al patrulea și, prin urmare, 243 în al cincilea.
Pe aceeasi tema:
Cuvintele pot construi copiii și îi pot distruge la fel de ușor. 25 de lucruri pe care să le spui copilului tău în fiecare zi 
Cu cât suntem mai buni, cu atât avem mai multe șanse ca lumea în care trăim să devină un loc mai bun 
Pielea ta ştie cel mai bine cât de fumătoare eşti 
Şi mie mi-e frică. Dar cel mai tare mi-e frică de…frică :)
